Every week, The Neopets Team (TNT) releases a new Lenny Conundrum puzzle. We will try to post the hints to solve the current Lenny Conundrum puzzle while we don't want to give out the answer directly. Sometimes, solution is given out by us. Other times, the puzzle is solved by others. In any case, we always put the solution so you have chance to guess the answer. Answer will be posted when the contest is over. So, please don't include a specific number/answer in the comments. We will also try to post all the previous solutions of the Lenny Conundrum puzzles.
We hope you enjoy our blog and if you have any feedback to improve our blogs, feel free to drop us a comment. Thanks.
Notice: There was a busy time that we thought we had to shut down this blog. Fortunately, we didn't. This is our plan until further notice.
Every Wednesday: we create an entry for those who are interested in discussion. We may or may not be here to put the solution up. If we are here, we will update the solution.
Every weekend: we will guarantee to put the solutions up by weekends, could be earlier than that. You can check back any time. You can use the following feature or feed feature for easier notice.






 Then we do integration on the whole vertical direction to add all area of the slices to get the volume. Since we choose the origin at the center of the sphere, the limit of the integration should be from -r to h-r
Then we do integration on the whole vertical direction to add all area of the slices to get the volume. Since we choose the origin at the center of the sphere, the limit of the integration should be from -r to h-r



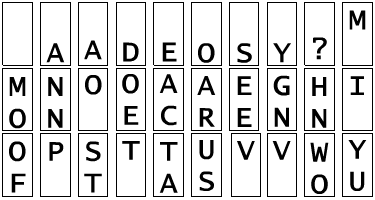
Same as round 257 except this is a trickier one. The question is: How many neopoints does a game of tyranu evavu cost? The answer is 30.
Results: 4335 people guessed the correct answer earning themselves 462 NP each.